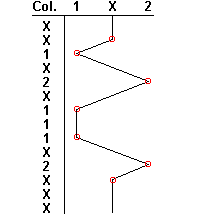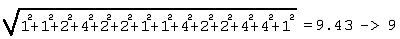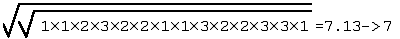Introduzione alla sistemistica Totocalcio
1. IntroduzioneNel Totocalcio è necessario indovinare il risultato di quattordici partite indicando con i segni 1, X e 2 rispettivamente la vittoria della squadre che gioca in casa, il pareggio, o la vittoria della squadra che gioca in trasferta. Le categorie di vincita sono tre:
In ogni schedina possono essere giocate fino a quattro colonne e in ogni colonna è possibile inserire delle varianti doppie o triple. Supponiamo ad esempio di voler giocare una colonna del tipo:
1X E’ facile convincersi che giocare questa colonna equivale a giocare le seguenti 12 che si ottengono sviluppando la precedente:
1 1 1 1 1 1 X X X X X X Queste 12 colonne formano il cosiddetto "sviluppo integrale" della colonna contenente le doppie e la tripla. Vediamo ora come si calcolano il numero di colonne facenti parte di uno sviluppo integrale, in base al numero di doppie e triple presenti in una colonna. Siano Nd, Nt, rispettivamente il numero di doppie e di triple, si ha: Numero di colonne = 2^Nd X 3^Nt Nell’esempio precedente avevamo Nd=2, Nt=1 ed infatti: Numero di colonne = 2^2 X 3^1 = 4 X 3 = 12 E’ facile costatare che all’aumentare di doppie e triple il numero di colonne cresce molto rapidamente, per esempio con 7 doppie e 2 triple avremo: Numero di colonne = 2^7 X 3^2 = 128 X 9 = 1152 pari a 576 Euro, sicuramente un costo elevato per la stragrande maggioranza dei giocatori. E’ qui che entra in gioco la sistemistica: il suo scopo è quello di eliminare dallo sviluppo integrale il maggior numero di colonne possibili in modo tale da rendere alla portata di tutti le giocate con pronostici molto ampi. Le colonne possono essere eliminate con tre metodi diversi: Sistema condizionato Utilizzando questa tecnica sono eliminate dallo sviluppo integrale tutte quelle colonne che non soddisfano determinate condizioni. Supponiamo di ritenere che le squadre che vinceranno fuori casa saranno almeno 1 e al massimo 2 e ed imponiamo una tale condizione al seguente pronostico:
1X2 Lo sviluppo integrale del pronostico precedente genera 4608 colonne che possono essere ridotte a sole 1952 colonne imponendo al sistema la seguente condizione: "Le colonne del sistema devono avere uno o due segni 2" In questo modo verranno scartare tutte le colonne che non contengono nessun segno 2 e quelle che ne contengono più di due. Esistono decine di modi diversi per imporre delle condizioni ad un sistema. Una descrizione dettagliata di queste condizioni è contenuta in questa guida in linea. Sistema ridotto Un altro metodo estremamente efficace per abbattere il costo di un sistema è quello di eliminare la colonne dallo sviluppo integrale utilizzando i l seguente criterio: scartare il maggior numero possibile di colonne dallo sviluppo integrale facendo in modo che nel caso in cui il pronostico consegua il 14, il sistema ridotto contenga almeno un 13 o un 12. Sistema condizionato ridotto Questo tipo di sistema deriva dalla combinazione delle due precedenti tecniche. Se si impongono alle colonne dell’integrale entrambe le tecniche avremo che, a pronostico e condizioni verificate, è garantita almeno la vincita di seconda o terza categoria, ovvero il 13 e il 12. Se, ad esempio, al sistema condizionato visto in precedenza applichiamo la riduzione N-1, otterremo un sistema che garantirà almeno il 13 se il pronostico non contiene errori e se la colonna vincente contiene 1 o due segni 2. 2. TerminologiaPer comprendere il funzionamento del programma sono necessarie alcune definizioni:
3. CondizionamentiTotoVision mette a disposizione tutti i più noti condizionamenti conosciuti in ambito sistemistico. Si può accedere ad essi dal menù condizioni o da un quadro multicondizione. Segue la descrizione sistemistica dei vari condizionamenti. 3.1 Numero di SegniIl numero dei segni permette di imporre alla colonne del nostro sistema di contenere una ben determinata quantità di segni 1, X e 2.
E' possibile inoltre specificare la consecutività nelle presenze dei vari segni ed il campo d'azione del condizionamento. 1 X 1 1 1 2 X X 2 X 1 X 2 X ha 5 presenze dei segni 1 con una consecutività pari a 3, 6 segni X di cui 2 consecutivi e 3 segni 2 nessuno dei quali è consecutivo (consecutività 1). 3.2 Consecutività DifferenziataQuesto tipo di
condizionamento permette di imporre alle colonne del sistema
una ben precisa consecutività di un segno a seconda della
quantità di segni presenti nella colonna in esame. 3.3 InterruzioniIn una colonna si ha un'interruzione quando si ha un cambiamento di segno da una casella a quella successiva
Consideriamo la seguente colonna: X 1 X 1 1 1 X 1 1 2 X 2 X X in essa sono presenti 9 interruzioni generiche di cui 4 consecutive, 3 interruzioni causate dal segno 1, 4 dal segno X e 2 dal segno 2. 3.4 VerticiDisponendo i segni di una colonna in modo analogo a quello delle schedine, cioè con i segni 1, X e 2 disposti su tre differenti colonne, si ottiene una spezzata il cui numero di vertici può essere condizionato. Questa condizione è disponibile in due versioni:
Esempio:
La precedente colonna ha sette vertici (pallini rossi) di cui tre causati dai segni 1, due dai segni X e due dai segni 2 3.5 Distanza SegniLa distanza tra due segni presenti in una colonna è data semplicemente dalla differenza delle loro posizioni. Ad esempio se in una colonna sono presenti due segni 2 alle posizioni 3 e 10 la distanza fra i segni sarà pari a 10-3 = 7.
Ad esempio consideriamo la colonna: 1 X 1 X X 2 1 1 1 X X 2 2 2 Avremo: Distanze del Segno 1
Distanze del Segno X
Distanze del Segno 2
Si tenga presente che nel caso in cui nella colonna non compaiano almeno due segni dello stesso tipo, le distanze per quel particolare segno avranno tutte il valore convenzionale zero. Ad esempio una colonna con un solo segno 2 avrà le tre distanze del segno 2 pari a zero. 3.6 Consecutività Pari e DispariIn una colonna
si conterà una consecutività pari (dispari) per ogni sequenza
di segni uguali di lunghezza pari (dispari). Per entrambi
è possibile impostare la consecutività nella presenza di tali
sequenze ed i campi d'azione dei due condizionamenti. X X 1 1 1 X 2 1 X X 2 2 X 1 in cui si contano 3 sequenze pari, di cui due consecutive, e 6 sequenze dispari di cui 4 consecutive. 3.7 SimmetrieUna simmetria è costituita da due caselle, in determinate posizioni della colonna, contenenti lo stesso segno. A seconda delle
coppie di caselle, utilizzate per i confronti, le simmetrie
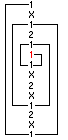
si dividono in dirette ed inverse. Esempio: D___D_______D______________ i_i_______i________________ le due colonne precedenti hanno rispettivamente 3 simmetrie dirette, nessuna delle quali consecutive (consecutività 1), e 3 simmetrie inverse due delle quali consecutive (consecutività 2). 3.8 VorticiSi tratta di un concetto sistemistico alquanto bizzarro che permette di associare ad una colonna due numeri, detti rispettivamente posizione e bracci del vortice ed un segno detto appunto segno del vortice. Esistono due tipi di vortice: quello diretto e quello inverso. Data una colonna, per calcolare la posizione del vortice diretto si prende inizialmente in considerazione il primo segno della colonna. Supponiamo ad esempio che si tratti di un segno 1: si cerca il segno in questione partendo dalla fine della colonna e si congiungono idealmente le due posizioni mediante una linea verticale. In seguito si cerca di nuovo il segno 1 partendo dalla parte alta (da una posizione successiva a quella iniziale) e si uniscono di nuovo le due caselle. La ripetizione alternativa di queste operazioni crea una ragnatela il cui centro è la posizione del vortice diretto, il numero di linee verticali tracciate rappresentano i bracci e il segno del vortice è quello presente nella casella data dalla posizione del vortice diretto. La procedura di calcolo del vortice inverso è del tutto analoga alla precedente con l'unica differenza data dal fatto che si parte dalla fine della colonna invece che dall'inizio. Esempio:
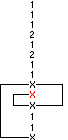
la precedente colonna possiede un vortice diretto alla posizione 6 (segno 1) e con un numero di bracci pari a 6. Per il vortice inverso si consideri la colonna:
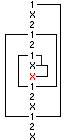
che ha il vortice posizionato alla casella 10 (segno X) con 3 bracci. Esistono anche colonne in cui il vortice non si chiude perfettamente, ovvero quando l’ultimo braccio non ha lunghezza 1. In questi casi è necessario scalare un posizione verso l'alto o verso il basso a seconda della direzione corrente della ricerca. L’esempio seguente illustra una situazione di questo tipo per un vortice diretto :
Come si vede dall’esempio precedente, l’ultimo braccio 1-1 ha lunghezza 3 e quindi il vortice non si chiude perfettamente. In una tale situazione è necessario scalare (tratto blu) una posizione verso il basso e far ripartire la ricerca dal segno X. 3.9 ModuloIl modulo è un condizionamento, con due varianti, assolutamente inedito ed ideato dall’Ing. Mauro De Ioris. Modulo Somma Il valore di questa condizione si calcola sostituendo ai segni 1, X e 2 della colonna, rispettivamente i numeri 1, 2 e 4. Così facendo al posto della normale colonna si otterrà una speciale colonna formata da 14 numeri. Un tale gruppo di numeri viene denominato Vettore. Calcoliamo il modulo somma per la colonna: 1 1 X 2 X X 1 1 2 X X 2 2 1 a tale colonna associamo il vettore: 1 1 2 4 2 2 1 1 4 2 2 4 4 1 ed infine calcoliamo il modulo:
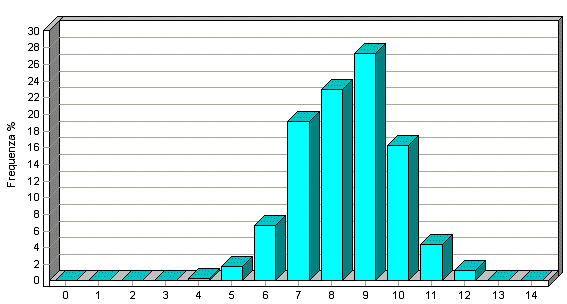
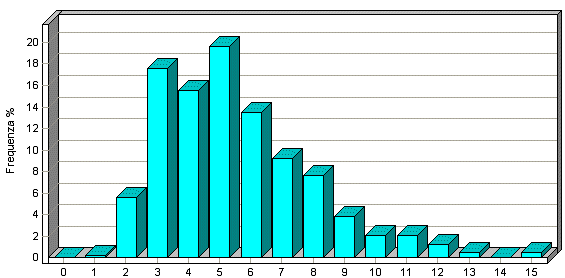
A questo punto dimostriamo l’efficacia sistemistica di questo condizionamento effettuando un'analisi statistica sulla sua frequenza ed un'analisi colonnare su un sistema di 14 triple: Analisi statistica:
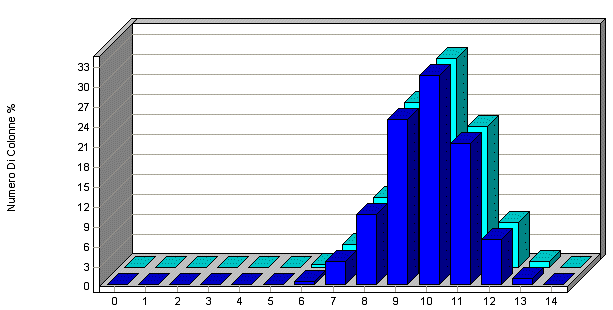
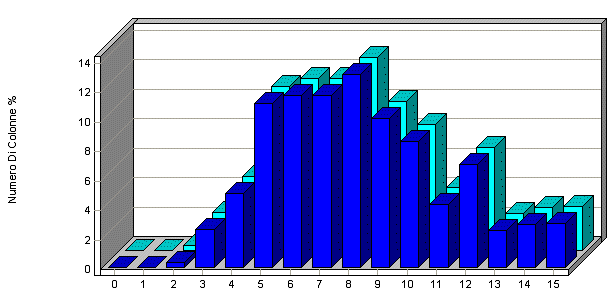
Analisi Colonnare delle 14 triple:
Come si vede dai due grafici precedenti i valori statisticamente più frequenti sono 7 ed 8 mentre i valori che danno più colonne per un sistema di 13 triple sono 9 e 10, quindi i due grafici sono notevolmente sfalsati: è proprio questa la caratteristica che assicura un ottimo rendimento statistico. Modulo prodotto In questo caso
ai segni 1, X e 2 si associano rispettivamente i numeri 1,
2 e 3. Colonna da esaminare: 1 1 X 2 X X 1 1 2 X X 2 2 1 associamo il vettore: 1 1 2 3 2 2 1 1 3 2 2 3 3 1 Il Modulo Prodotto è quindi:
Analisi statistica:
Analisi colonnare delle 14 triple:
Anche in questo caso si può osservare come i due grafici siano notevolmente sfalsati: le frequenze assumono i valori massimi in corrispondenza dei valori 3,4 e 5 mentre i valori più frequenti nelle 14 triple si hanno per i valori 6, 7 ed 8 3.10 Formule DerivateUna formula
derivata è semplicemente la terna di numeri corrispondente
alla quantità dei segni 1, X e 2 presenti in una colonna. 1 2 1 1 X X X 1 2 1 1 X 2 X è la 6-5-3. 3.11 RipetizioniLe
ripetizioni scaturiscono dal confronto delle colonne del sistema
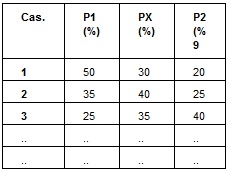
con le colonne degli ultimi due concorsi presenti in archivio. Ad esempio supponiamo che la colonna dell’ultimo concorso presente in archivio sia la seguente: Ultimo concorso: 1 1 1 X X 2 X 2 1 1 1 X 2 X se la colonna da esaminare è 1 1 X 1 1 X 2 X 1 X 1 X 2 1 avremo 6 ripetizioni, di cui 3 consecutive, sull'ultimo concorso presente in memoria Il confronto può anche essere effettuato su più concorsi simultaneamente. Se ad esempio richiediamo il confronto con gli ultimi tre concorsi presenti in archivio, le colonne del sistema verranno confrontate con tutte e tre i concorsi e la generica colonna del sistema verrà accettata solo se i punteggi realizzati da queste tre colonne saranno compatibili con quelli richiesti. Supponiamo ad esempio di richiedere che le colonne del sistema abbiamo da 3 a 6 punti in comune con le ultime tre colonne presenti in archivio : Ultimo concorso: 1 1 1 X X 2 X 2 1 1 1 X 2 X Ultimo concorso: 1 1 1 X X 2 X 2 1 1 1 X 2 X Ultimo concorso: 1 1 1 X X 2 X 2 1 1 1 X 2 X se la colonna da esaminare è ancora: 1 1 X 1 1 X 2 X 1 X 1 X 2 1 avremo 6 ripetizioni sull’ultima colonna, 7 sulla penultima e 4 sulla terzultima. In questo caso la colonna verrebbe scartata perché la condizione è soddisfatta solo sull’ultimo e sul terzultimo concorso mentre il penultimo realizza 7 punti che rappresentano un valore non compreso nel range richiesto (3-6). Questa condizione può lavorare anche in modalità somma : in questo caso verranno sommati i punteggi realizzati confrontando le colonne presenti in archivio con la colonna da esaminare e tale somma potrà essere condizionata imponendo un valore minimo ed uno massimo. Con riferimento all’esempio precedente, supponiamo di aver richiesto che la somma delle ripetizioni rispetto agli ultimi tre concorsi debba essere compresa tra 12 e 20. In questo la colonna verrà accettata perché la somma delle tre ripetizioni, pari a 6+7+4=17, risulta compresa tra 12 e 20. 3.12 Sezioni OrdinateLe sezioni ordinate sono una generalizzazione delle metodologie Futuro e Section. Questo condizionamento opera nel seguente modo : la colonna totocalcio viene suddivisa in una o più sezioni. Le più comuni suddivisioni sono, ad esempio, le 4 terzine nelle posizioni 1, 4, 7 e 10 o le classiche 7 accoppiate nelle posizioni 1,3,5,7,9,11. Data una sezione, ad esempio la prima terzina 1-3, ed un picchetto percentuale, è possibile associare ad ognuna delle 27 terzine (o colonnine) che si possono formare con 3 segni, una ben precisa probabilità di uscita data dal prodotto delle probabilità dei segni. Supponiamo ad esempio di avere il seguente picchetto percentuale :
La probabilità di uscita della terzina X 2 2 sarà data da : 30x25x40 / 100 / 100 = 3 % Dopo aver associato una probabilità ad ognuna delle 27 terzine, possiamo ordinarle dalla più probabile (la numero 1) alla meno probabile (la numero 27). A questo punto, ogni terzina del nostro sistema sarà caratterizzata dalla sua posizione nell'ambito di questo ordinamento. Impostando ad esempio le posizioni 1-10, chiederemo al sistema di ammettere, nella sezione 1-3 delle colonne, soltanto le terzine che, nell'ordinamento probabilistico dato dal picchetto corrente, sono posizionate nelle prime 10 posizioni. Esiste anche una seconda modalità di utilizzo di questo condizionamento : invece di indicare le posizione da ammettere si specifica l'intervallo di probabilità che queste devono coprire. Per meglio comprendere questo concetto analizziamo il seguente ordinamento :
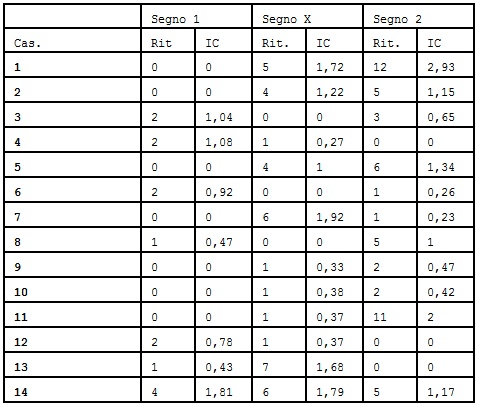
Focalizziamo l'attenzione sulle ultime due righe che riportano rispettivamente le probabilità di ogni singola terzina e la probabilità totale di tutte le terzine fino a quella posizione. Per esempio, nella terza posizione avremo una probabilità pari al 7% e una probabilità totale delle prima 3 posizioni data dalla somma 8+7+7=22 %. 3.13 Somme delle PosizioniQuesta condizione somma le posizioni dei segni 1, X e 2 all'interno di una colonna totocalcio Ad esempio se, in una colonna sono presenti due segni X nelle caselle 3 e 10, la somma delle posizioni dei segni X sarà pari a 10+3 = 13. Vediamo un altro esempio : 1 X 1 X X 2 1 1 1 X X 2 2 2 Avremo: Somma delle posizioni dei Segni 1 : 1+3+7+8+9 = 28 3.14 BaricentriIl baricentro di un dato segno, in una colonna totocalcio, è dato dalla somma delle posizioni che lo contengono, diviso il numero di occorrenze del segno nella colonna. Il valore ottenuto da questa divisione deve poi essere privato degli eventuali decimali. Vediamo un esempio : 1 1 1 X 2 X 1 1 2 X X 2 2 1 Avremo : Baricentro dei Segni 1 : (1+2+3+7+8+14) / 6 = 35 / 6 = 5.8 -> 5 3.15 Somma dei Ritardi e degli ICIn ogni concorso i 42 segni (14*3) hanno un ben preciso ritardo ed IC. Grazie a questa condizione è possibile sommare i ritardi o gli IC associati a ciascun segno della colonna ottenendo un valore totale che può essere condizionato con un valore minimo ed uno massimo. Supponiamo ad esempio che i valori dei ritardi e degli IC, per un dato concorso, siano i seguenti :
Allora per la colonna : 1 X X 1 X 2 1 X 1 X 1 1 2 X Avremo le seguenti somme : Somma dei ritardi : 0+4+0+2+4+1+0+0+0+1+0+2+0+6 = 20 3.16 PercentualiMediante questo condizionamento è possibile associare ad ogni colonna un numero dato dalla probabilità, espressa in percentuale, che gli eventi selezionati nella colonna risultino verificati. Per calcolare la probabilità del verificarsi di più eventi è necessario effettuare il prodotto delle rispettive probabilità. Supponiamo ad esempio che gli eventi selezionati siano i primi tre e che le percentuali contenute nel picchetto alle prime tre righe siano: 50 35 15 allora la colonna 1 X 2 1 1 1 X 1 1 2 1 1 1 X avrà una probabilità pari a 50*40*10 / (100*100) = 2% 3.17 Valori SquadraIl condizionamento permette di associare ad ogni colonna un numero dato dalla somma dei valori associati ad ogni segno nelle partite selezionate. Supponiamo ad esempio che le partite selezionate siano le prime tre e che i valori attribuiti ai segni, contenuti nella schedina posta sul desktop, per le prime tre partite siano: 250 345 109 allora alla colonna: X 1 2 1 1 1 X 1 1 2 1 1 1 2 sarà associato il numero 345+135+105. 3.18 Punti SquadraIl condizionamento punti squadra permette, dato un gruppo qualsiasi di squadre, di condizionare il numero di punti realizzabili da queste. In pratica ad ogni colonna viene associato un numero dato dalla somma dei punti realizzati dalle squadre selezionate come se la colonna in questione fosse quella vincente. Alla vittoria è possibile attribuire un numero di punti pari a 2 o 3 mediante la funzione Impostazioni Varie. Esempio: se le squadre selezionate sono la prima della prima casella, la seconda della terza casella e la prima della quarta casella, alla colonna: 3___3_1____________________ saranno associati 7 punti. 3.19 SequeleUna sequela non è altro che una sequenza contigua di segni di lunghezza arbitraria. Le sequele sono caratterizzate dal modo con il quale vengono cercate all'interno della colonna da analizzare e dai segni che contengono. La ricerca di una sequela di lunghezza Y in una colonna avviene nella seguente maniera: 1) si confronta la sequela in esame con quella presente ai primi Y posti della colonna. 2) se la sequela viene trovata si incrementa la posizione della casella nella quale cercare la sequela di un valore detto "Passo Trovata". 3) se la sequela non viene trovata l'incremento è dato dal "Passo non Trovata". 4) si ritorna al punto 1) cercando però la sequela non dalla 1º posizione ma da quella calcolata con i passi precedenti. Alcuni passi hanno dei nomi particolari, i più noti sono:
Per quanto riguarda la caratterizzazione in base ai segni abbiamo i seguenti tipi di sequele
1 1 X 1 2 2 1 1 X 1 1 X 1 1 avremo 4 presenze della sequela 11 che è quella maggiormente presente. Specchi: Gli specchi sono coppie di sequele di uguale lunghezza aventi i segni disposti a specchio fra loro. Esempio: *****______*****___________ nella colonna in esame sono contenuti due specchi di lunghezza 3 dati dalle coppie (1X2, 2X1) e (11X, X11). 3.20 Colonne FiltroQuesto condizionamento viene utilizzato per confrontare le colonne del sistema con una colonna, detta appunto filtro, immessa dall'utente, ed imporre che le tali colonne abbiano un certo numero di segni in comune con la colonna filtro. Una colonna filtro non deve essere necessariamente composta da tutti i 14 segni e può inoltre contenere doppie e triple. Esempi di colonne filtro sono:
1 2 1 3.21 Quadri MulticondizioneUn quadro multicondizione è un particolare tipo di condizionamento che al suo interno può contenere un gruppo di condizioni di qualsiasi tipo, compresi ulteriori quadri, con la possibilità di imporre alle colonne del sistema di verificare un numero arbitrario di queste condizioni. Le principali applicazioni di questa struttura sono:
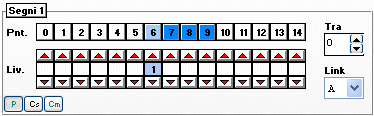
3.22 Link e livelli di recuperoIl livello di recupero di un punteggio specifica quanti errori possono essere recuperati tra tutti i punteggi ammessi in recupero a tale livello. Ad esempio se un punteggio di una condizione è ammesso in recupero al livello 2 e la colonna in esame consegue proprio tale punteggio, l'errore eventualmente occorso verrà recuperato solo se tra tutti i punteggi, di qualsiasi condizionamento contenuto nella link, ammessi in recupero allo stesso livello, saranno stati effettuati non più di 2 recuperi. E' possibile condizionare il numero di errori che possono essere recuperati nell'ambito delle condizioni contenute in una stessa link e nell'ambito di tutti i condizionamenti contenuti in tutte le link utilizzate. Cerchiamo di chiarire meglio questi concetti con un esempio pratico: Consideriamo un semplice sistema formato da due sole condizioni: il numero dei segni 1 e le interruzioni. Il numero dei segni 1 è impostato nel seguente modo:
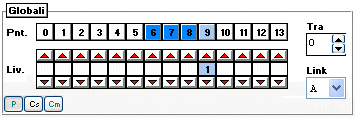
con i punteggi 7,8 e 9 ammessi e con il 6 posto in recupero a livello 1. Le interruzioni globali sono imposte da 6 a 8 e con il punteggio 9 in recupero sempre a livello 1.
In questo caso entrambe le condizioni sono contenute nella Link A e non vengono utilizzati i punti Tra: infatti in entrambe le condizioni il gruppo Tra è impostato a zero (nessun gruppo). Consideriamo i seguenti casi: Supponiamo che la colonna in esame abbia le seguenti caratteristiche:
Nel primo caso la colonna non viene scartata perché i punteggi 7 e 8 sono entrambi ammessi (colore blu) nelle rispettive condizioni. Nel secondo caso i 7 segni 1 sono ammessi (colore blu) mentre le 9 interruzioni sono in recupero (colore azzurro). La colonna non viene scartata perché l’errore commesso viene recuperato in quanto nella Link A al livello 1 è stato commesso un solo errore. Infine nel terzo caso abbiamo entrambi i valori in recupero e, siccome si trovano a livello 1, la colonna viene scartata perché nella Link A sono stati commessi due errori nel livello 1. In pratica tra tutti i punteggi a recupero a livello 1 se ne può sbagliare al massimo uno nell’ambito della stessa link. 3.23 Super LinkIn un sistema che utilizza molti livelli di recupero in Link differenti può risultare utile condizionare il numero di totale errori che si verificano agli stessi livelli ma in Link differenti. Supponiamo ad esempio di aver un sistema che utilizza livelli di recupero 1 e 2 nelle link A,B,C, D ed E. E’ noto che, tra tutti i punteggi a recupero a livello 1 di ogni Link, possiamo compiere un solo errore. Quindi a livello 1 potremo compiere 5 errori (uno per ogni link) ed al livello 2 potremo compiere altri 10 errori (due per ogni link). L’uscita di una colonna che recuperi tutti questi errori è teoricamente possibile ma realisticamente alquanto improbabile. Grazie alle Super Link possiamo limitare il numero di questi errori che si verificano in Link differenti. Nell’esempio visto prima potremo richiedere al programma che al livello 1 tra tutte le Link si verifichino 0-3 errori e che, ad esempio, al livello 2 si verifichino 3-8 errori. Questo potente condizionamento ci permette anche di limitare gli errori che si verificano complessivamente in diversi livelli presenti in varie Link. Potremo ad esempio imporre al nostro sistema di compiere da 5 a 15 errori tra i livelli 1, 3 e 5 presenti nelle link A,B,C, D ed E. Le Super Link non vanno confuse con le normali Link dove è possibile condizionare solo il numero di errori presenti in TUTTI i livelli di una determinata Link. Con le Super Link è invece possibile indicare anche quali livelli considerare ed in quali Link questi devono essere contenuti. 3.24 Punti TraI punti tra sono ottenuti sommando i punteggi realizzati nelle presenze o nelle consecutività di un gruppo di condizionamenti. Ogni gruppo è individuato da un numero compreso tra 1 e 30: per far si che una condizione sia contenuta in un certo gruppo è necessario che nel box dei punteggi del condizionamento si specifichi il numero del gruppo desiderato. Supponiamo ad esempio che nel Gruppo Tra 1 siano contenute le presenze dei segni 1 e quelle delle interruzioni globali: se le prime realizzano 7 punti e le seconde 6, il punteggio Tra realizzato dal gruppo 1 sarà semplicemente 7+6=13. 3.25 Gemelli TraIl condizionamento Gemelli Tra permette di specificare quanti punteggi dello stesso tipo sono presenti nelle colonne del sistema. Ad esempio è possibile imporre una condizione secondo la quale, tra tutti i punteggi inseriti nel gruppo Tra 1, può essere presente al massimo un punteggio “5”. Se nel gruppo Tra 1 sono state inserite le condizioni Numero di Segni X, Interruzioni Globali, Simmetrie Dirette, una colonna che abbia 5 segni X, 5 interruzioni e 2 simmetrie verrebbe scartata mentre una colonna con 4 segni X, 5 interruzioni e 2 simmetrie verrebbe accettata perché contenente un solo punteggio 5. 4. FiltroriduzioneLa filtroriduzione è una tecnica per ottenere sistemi ridotti utilizzando particolari colonne filtro, dette appunto riduttori, adatte allo scopo. Dato che le colonne filtro dei riduttori sono riferite ad un particolare pronostico, è necessario adattarle al proprio mediante la funzione Adatta disponibile nel menù pop up dei quadri multicondizione. E' stata scoperta una vasta gamma di riduttori e molti di questi sono disponibili in Totovision mediante files di condizioni (in questo caso solo colonne filtro) aventi il seguente formato: nella prima colonna è contenuto il pronostico (o parte di esso) rispetto al quale le colonne del riduttore sono riferite e nelle successive colonne sono contenute le colonne filtro vere e proprie. La colonna contenente il pronostico verrà automaticamente eliminata dopo l'adattamento. Consideriamo ad esempio il classico riduttore 7 doppie:
1X X Come si vede il precedente riduttore è riferito ad un pronostico formato da sette doppie 1X posizionate nelle prime 7 posizioni. Mediante la funzione Adatta potrà essere facilmente adattato ad un pronostico che ha le doppie di qualsiasi tipo e in qualsiasi posizione. Chiaramente se abbiamo un pronostico formato da più di 7 doppie, il riduttore sarà comunque utilizzabile: sarà sufficiente specificare le 7 doppie sulle quali deve agire il riduttore ed utilizzare poi la funzione Adatta. |